[논문 리뷰] Generative Adversarial Nets - GAN

 

GAN에 대한 논문 리뷰를 해보자!

 

논문 링크.

Generative Adversarial Nets

 

참고한 블로그

(GAN)Generative Adversarial Nets 논문 리뷰

 

세줄 정리.

1. D,G를 사용한 생성형 모델 GAN을 제안함.

2. V(G,D)의 minmax의 학습 방식으로 수식을 제안함.

3. 이론적 배경을 수학적으로 증명하는 방식이 흥미로움.

 

0. Abstract

G: data distribution를 생성하는 모델: Generative model

D: Real data와 Generative data를 구별하는 모델: Discriminative model

-> 엄밀하게는 D는 real data인지 판단하는 확률을 추정한다.

G는 D가 판별하지 못하게 학습한다. 그리고 D는 이를 잘 구별하기 위해 학습한다.

이렇게 minimax two-player game이 진행되면서, G는 training data distribution를 학습하게 되고, D의 값는 1/2로 수렴하게 된다. 즉 진짜와 가짜를 구별할 수 없게 되는 것이다.

GAN는 multilayer perceptron으로 표현이 가능해서, back propagation으로 학습이 가능하다.

1. Introduction

기존의 Deep generative model는 한계가 존재한다. 

1) 확률 근사하기가 어렵다.

the difficulty of approximating many intractable probabilistic computations that arise in maximum likelihood estimation

2) 선형 활성화 함수를 다루기 어렵다.

the difficulty of leveraging the benefits of piecewise linear units in the generative context.

GAN는 비유하자면, 위조화폐를 만들어내는 G와 이를 판별하는 경찰 D로 볼 수 있다.

GAN는 backpropagation, dropout algorithms, forward propagation만으로도 학습이 가능하다.

 

2. Related work

위 내용과 비슷해요~

 

3. Adversarial nets

변수 정의

pg: generative를 통해 생성한 data

p(z) : 임의의 입력값(random noise) z

G(z): 임의의 입력값을 기반으로 θg 파라미터로 학습하여 생성하는 모델.

D(x): x가 real data에서 나왔는지 판별할 확률을 추정하는 모델.

 

Value Funtion: V(G,D)

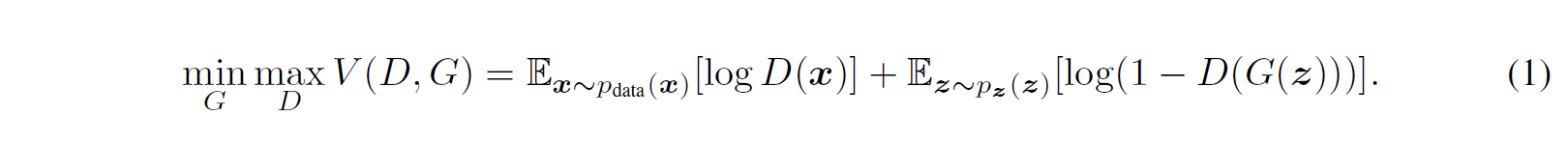
학습은 크게 두 가지 방식으로 진행된다.

D를 Maximize하는 방식와 G를 Minimize하는 방식이다.

이 뜻이 무엇이냐면

D를 Maxmize: 진짜를 진짜라고, 가짜를 가짜라고 판별을 더 잘하게 하는 것.

즉 real data를 D(real data) = 1이 되도록 학습하고 D(fake data) = 0 이 되도록 학습하는 것이다.

D(real data) = 1, 1-D(fake data) = 1 이 되도록 최대화 되도록 학습한다. (1에 가깝게 하는 것이 최대화한다는 의미)

G를 Minimize: D가 가짜를 진짜로 판별하도록 하는 것

즉 D(G(z)) = 1 이라고 학습하게 하는 것

1-  D(G(z)) = 0 이 되도록 최소화되도록 학습한다. (0에 가깝게 하는 것이 최소화한다는 의미)

 

식으로 들어가보자.

첫째 항: 

logD(x)

D의 입장: real data를 1로 판단하도록 첫째항의 값이 최대화.

 

둘째 항: log(1-D(G(z)))

D의 입장: fake data G(z)를 0으로 판단해서 둘째항의 값이 최대화.

여기서 보면 알겠지만, D의 입장에서 최대화한 이상적인 값은 log1 + log1로 0이다.

G의 입장: 1- D(G(z))를 0로 판단해서 둘째항의 값이 최소화. (쉽게 생각하면 D(G(z)) =1로 최대화 하는 것, 의미론적으로는 1-D(G(z)) = 0 가 맞음)

G의 입장에서 최소화한 이상적인 값은 log?(첫째항은 관련없음) + log0로 -무한대이다.

 

이론적인 수식은 위와 같이 학습을 진행하게 되면, pg = pdata 가 되지만, 실제로는 실질적인 문제에 봉착하게 된다.

D가 과적합(overfitting)하는 문제가 발생한다. 이는 초반에 G의 성능이 매우 떨어지기 때문에, D가 학습이 너무 잘되기 때문이다. 이를 해결하기 위해서.

1) D를 k step optimize하고, G를 one step optimize하는 방식으로 진행한다. 이는 D가 충분히 최적화된 상태에서, G가 너무 급하게 이상하게 학습되지 않도록 천천히 학습될 수 있도록 한다.

*내가 이해한 바에 의하면 overfitting의 문제는 D에서 발생하지만, 결국 G의 성능에 영향을 미치는 factor로 이해하기 좋다. 이것이 무슨 말이냐면, D가 너무 잘 판별해서 overfitting이 일어났을 때, 사실 D는 크게 상관이 없다. 왜냐하면 잘 판별했다는 것을 좀 급하게 학습했을 뿐이지, input data가 애초에 구분하기 너무 쉬우면 어느정도의 빠른 학습이 일어나는 것은 당연하기 때문이다. 그래서 결국 G가 fake data를 잘 만들어내는 것이 관건인데, D가 너무 빨리 학습된 바람에 G가 올바르게 학습하는 것이 아니라, 계속 D의 속도를 맞추기 위해 이상한 부분들에서 판별하지 못하게끔 잘못된 포인트로 data를 생성한다고 이해하였다. 그래서 G의 성능이 낮게 나오는 것이다. 그래서 결국 마지막 한 문장으로 정리하자면, 최적화된 D의 상태에서 G를 천천히 학습해야하는 의미론적 이유가 overfitting된 D에 맞춰 G를 학습시키지 않기 하기 위해서다. 라고 정리할 수 있겠다.

2) 초반에 1-D(G(z))를 min하는 것보다, logD(G(z))를 max하는 방식으로 학습한다. 1-D(G(z))를 min하는 방식으로 학습하는 것은 기울기 소실을 보일 수 있다. 왜냐하면 애초에 log(1-0) 꼴로 값이 매우 작기 떄문에 학습하는 정도가 매우 작을 것이기 때문이다. 반대로 logD(G(z))를 max하는 것은 큰 기울기 값을 가져올 수 있을 것이다.

 

검은선: real data distribution

파란선: discriminative distribution

초록선: generative distribution

(a) D가 아직 오락가락한 상태. 아직 G는 real data랑 다르다.

(b) D가 최적화 된 상태. 아직 G는 real data랑 다르다.

(c) D가 최적화 됨. G가 real data랑 비슷하게 학습 중이다.

(d) D가 최적화 됨. G가 real data랑 똑같은 분포로 수렴한다. pg = pdata인 상태. D(x) = 1/2

 

4. Theoretical Results

추가적으로 증명을 해야 하는 부분들이 있다.

1) pg = pdata 일 때 minmax V(G,D)의 최적화 된 값이 임을 증명해야 한다.

2) 최적화되는 과정 속에서 V(G,D)의 값이 pg = pdata로 수렴하는 것을 증명해야 한다.

 

4.1 Global Optimality of pg = pdata

G를 고정한 상태에서 D를 최적화 할때의 식을 먼저 구한다.

D를 먼저 최적화한 식을 구하는 이유를 생각해보았는데, D가 G보다 학습이 빠르기 때문이라고 생각했다. D를 최적화가 더 빠르기 때문에, G를 일단 배제하고(고정하고) G로 이루어진 식을 구하는 것이다.

즉 현재의 G 상태에서의 최적화된 D 식을 구하여, 학습 시 G를 할 수 있도록 한다.

이런 꼴의 식이 나오게 된다. alogx+blog(1-x)의 최댓값은 x= a/a+b일 때 이다. 

즉,

일 때 최적화되는 것을 알 수 있다.

이제 식에 D값을 넣으면 다음과 같다.

바뀐 식 C(G)가 pg=pdata일 때 최소값을 갖는 것을 증명한다.

먼저 pg = pdata를 넣어보자.

-log4가 나오는 것을 확인할 수 있다. 이제 다른 방식으로 -log4보다 더 큰 값을 나타낼 수 있는 지 확인해보자

더 작아질 수 있는지 확인해보는 것이다.

C(G)는 다른 방식으로 나타내면 다음과 같이 표현할 수 있다.

JSD식은 다음과 같다.

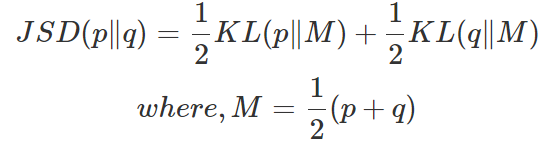
JSD 값은 0보다 크거나 같기 때문에 결국 -log4, 즉 pg=pdata일 때 최소값을 갖는 것을 확인할 수 있다.

 

4.2 Convergence of Algorithm1

이제 pg가 pdata로 수렴한다는 것을 증명해보자.

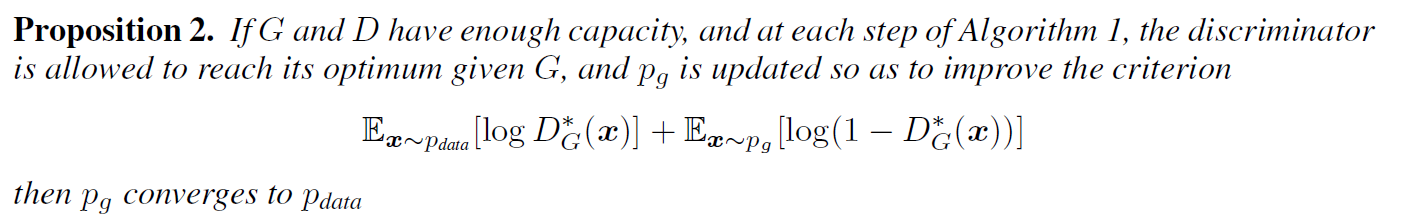
G,D가 이론적으로 data가 많을 때 위의 수식이 pg -> pdata로 수렴하는 지를 확인해보자.

이유가 다음과 같다. 너무 수학적인 이야기라 좀 어려운데.

이해한 바에 따르면, V(G,D)는 결국 pg로 수식을 표현할 수 있고, 이는 pg에 대해서 위로 볼록한 함수다.(Convex function)

따라서 학습을 하게 되면, 충분히 pg -> pdata로 수렴할 수 있다 라고 이해했다.

그리고 실제론, pg를 모르기 때문에, pg 대신 파라미터 θg를 사용한다. 이는 엄밀히 봐서는 증명한 부분은 아니지만, 합리적인 접근로 보았다. (reasonable model to use despite their lack of theoretical guarantees)

 

5. Experiments

MNIST, Toronto Face Database, CIFAR-10

1)

실제분포에서 생성한 그림들이다.

 

6. Advantages and disadvantages

Advantage

Statistical advantage 존재.

매우 선명한 이미지를 생성할 수 있다.

 

Disadvantage

pg(x)의 데이터 분포를 명시적으로 알 수 없다. 

D는 학습 시에 G랑 조화롭게 synchronized하게 학습해야 한다.

 

7. Conclusions and future work

A conditional generative model: 조건부 모델 개발

Learned approximate inference: 역으로 z를 추론하는 모델 개발

training a family of conditional model that share parameters: condition model를 근사할 수 있음

Semi-supervised learning: 반지도 학습

Efficiency improvements